Comment les Grecs mesuraient la distance de la Terre à la Lune et au Soleil

Avant de commencer, posons-nous la question : si l’on vous demandait aujourd’hui de calculer ces distances, ou le diamètre de la Lune ou du Soleil, comment vous y prendriez-vous ? C’est là qu’apparaît toute l’inventivité des savants Grecs de l’Antiquité, à la fois observateurs, astronomes, inventeurs et géomètres…

Le premier pas: connaître le diamètre de la Lune

Dès le 6e siècle av. J.-C., les Grecs (Parménide, Platon, Aristote) admettaient que la Terre était sphérique (comment expliquer autrement l’horizon ? Et n’est-ce pas la forme divine idéale ?), et que c’était son ombre qui expliquait les éclipses de Lune. Aristarque de Samos (env. 310-230 av. J.-C.) avait observé combien de temps la Lune disparaît derrière l’ombre de la Terre. Il suffit d’un sablier pour cela.

Il en déduit que le diamètre de la Lune est environ 3 fois plus petit que celui de la Terre. Ce qui est astucieux, mais inexact, car cela suppose que les rayons du Soleil arrivent tous parallèlement, et donc que la zone d’ombre portée par la Terre est cylindrique.
C’est Hipparque (env. 190-120 av. J.-C.) qui précisa ce diamètre en découvrant que la projection de l’ombre de la Terre est conique et non cylindrique: il corrigea la valeur ci-dessus à 4 fois, ce qui est assez proche de la réalité. Encore fallait-il connaître le diamètre de la Terre.

Calcul de la circonférence de la Terre

Aristote, au 4e siècle av. J.-C., l’évaluait à 60 000 km, mais c’est Eratosthène (276-194 av. J.-C.), conservateur de la bibliothèque d’Alexandrie, qui l’évalua avec une extraordinaire précision.
Sa méthode est souvent citée comme modèle de la démarche scientifique des Grecs: il avait remarqué qu’au solstice d’été (le 21 juin), le Soleil tombait à la verticale dans un puits situé à Syène (aujourd’hui Assouan). Ceci n’arrivait pas à Alexandrie, où l’ombre d’un obélisque gardait, par rapport à la verticale, un angle de 7,2°. La Terre étant sphérique et Assouan étant au sud d’Alexandrie (pratiquement sur le même méridien), il suffisait de connaître la distance entre les deux villes pour en déduire le diamètre de la Terre. Ce que fit Eratosthène en comptant les pas des chameaux, aboutissant (malgré quelques erreurs, qui par chance se compensaient !) à une circonférence terrestre de 39 375 km, toute proche de la réalité.

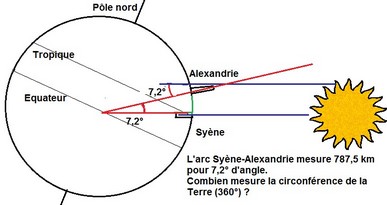
Voici la figure géométrique qui explique le calcul d’Eratosthène
(là aussi, on considère que les rayons du soleil sont parallèles entre eux).

Calcul de la distance Terre-Lune

Archimède avait inventé, dès le 3e siècle av J.-C. le « dioptre », un instrument rudimentaire composé d’une règle graduée qui portait à son extrémité une petite plaque percée d’un trou servant d’oculaire, et 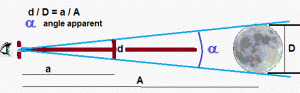un élément coulissant d’une largeur bien définie. En déplaçant celui-ci jusqu’à ce qu’il cache l’objet visé (la Lune), un petit calcul trigonométrique permettait de définir l’angle apparent sous lequel se présente l’astre. Connaissant le diamètre de la Terre, donc celui de la Lune, un autre petit calcul de proportionnalité aboutit à la distance Terre-Lune. Notons qu’Aristarque de Samos avait déjà appliqué cette méthode, mais il lui manquait cette donnée essentielle: le diamètre de la Terre. Il pouvait juste dire que cette distance était d’environ 40 diamètres terrestres.

Et la distance de la Terre au Soleil ?

Là aussi, il suffit de remarquer comme Aristarque (y auriez-vous pensé ?) que, lors d’une parfaite demi-lune, le Soleil l’éclaire « de côté », ce qui signifie qu’il forme avec la Terre et la Lune un triangle rectangle.

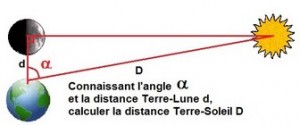 Connaissant l’angle sous lequel se trouve alors le Soleil et la distance Terre-Lune, on définit la distance de la Terre au Soleil. Et comme on connait aussi le diamètre apparent de ce dernier, on peut en déduire son diamètre… Qui semble bien sûr énorme !
D’où on déduit que l’ombre de la Terre n’est pas un cylindre, mais un cône, etc. etc.

Et si la Terre tournait autour du Soleil ?

Aristarque (encore lui) avait déjà subodoré la chose: il lui semblait logique que les petits astres tournent autour du plus gros, comme la Lune autour de la Terre, mais sa théorie ne s’imposa pas, et Archimède lui rétorqua d’ailleurs que la Terre est solide et donc plus lourde que le feu du Soleil, aussi gros soit-il. Tout le monde peut se tromper, et le modèle géocentrique de Claude Ptolémée (90-168), fort habilement conçu il est vrai – mais ceci est une autre histoire – s’imposa pendant 13 siècles.

Les conséquences de ces travaux

Eh bien, on peut en déduire que les Grecs étaient de grands observateurs et de grands géomètres, même si leurs résultats sont souvent approximatifs… Peu importe car pour eux, la démarche compte au moins autant que le résultat.
Un résultat qui aurait pu cependant être fort utile à Chistophe Colomb, mais cela n’a pas intéressé grand monde pendant des siècles : que la Terre fut plate ou immobile, la belle affaire au regard des évangiles ! Il faudra attendre Copernic pour en savoir plus…