Les figures géométriques dans l’Antiquité: ornements ou symboles?

Dès la préhistoire, les hommes ont dessiné ce qu’ils voyaient autour d’eux, des personnages, des animaux, des plantes, mais aussi des figures abstraites dont on ne peut saisir la signification, sinon que leur simplicité et leur symétrie devaient paraître belles, et que cette beauté leur donnait un sens.

Typologie des signes du paléolithique
supérieur en France, G. von Petzinger

Il est vrai que ces figures se trouvent dans la nature sous des formes variées (la Lune et le Soleil pour le cercle, les coquillages et les végétaux pour la spirale, les faces planes sur les cristaux, etc.).

C’est peut-être justement ce qui en fait l’universalité, et donc la magie de l’abstraction.

Fibule de l’âge de bronze,
Europe centrale,
8e-7e siècle av. J.-C.

Parmi les figures simples se trouvent la croix, le cercle et le rectangle et surtout, représentée par toutes les civilisations, la spirale, une forme qui s’ouvre ou se referme selon la manière dont on la regarde. Comment s’étonner que les hommes tracent alors la spirale double qui s’ouvre ET se referme, donnant ainsi une image de l’infini…

Les Anciens s’intéressent aussi aux polygones réguliers comme le triangle équilatéral, le carré, et plus tard le pentagone et l’hexagone, ainsi qu’à leurs variantes, les polygones étoilés à 5 ou 6 branches.

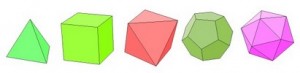
Les volumes comme la sphère et les polyèdres ne sont pas en reste. Fascinés par la beauté de la simplicité géométrique, les Grecs ont défini les « solides de Platon », des polyèdres qui leur semblaient parfaits.

Sur le tétraèdre (4 faces), l’octaèdre (8 faces) et l’icosaèdre (20 faces), chaque face est un triangle équilatéral. Toutes les faces du cube sont un carré, toutes celles du dodécaèdre (12 faces) sont un pentagone.

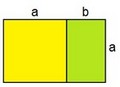Ils ont aussi étudié le « nombre d’or » qui donne la proportion la plus harmonieuse au rectangle (la « divine proportion »). En clair, si l’on découpe un carré dans celui-ci, le petit rectangle restant garde la même proportion que le rectangle d’origine, c’est-à-dire que b/a = a/(a+b). Saurez-vous le calculer ? Les Egyptiens l’auraient également connu, mais c’est un autre polyèdre, la pyramide à base carrée, LA pyramide, qui leur est associée le plus souvent ! Ils avaient aussi remarqué les propriétés du 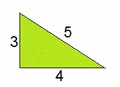triangle rectangle dont les côtés mesurent respectivement 3, 4 et 5 unités de longueur appelé parfois « triangle sacré ». Il vérifie bien sûr le théorème de Pythagore, puisque 3² + 4² = 5².

Géométrie et magie

Le plus curieux est de constater combien ces signes, en dehors de toute considération géométrique et esthétique, ont été chargés, au fil des siècles, de significations symboliques, religieuses, magiques et occultes.

Dans l’étoile à cinq branches, le pentagramme, certains voient le symbole du diable, de l’homme… ou du divin. Il est aussi nommé pentacle et, souvent inscrit dans un cercle, devient alors le signe protecteur d’une amulette. L’étoile à six branches est devenue le symbole du judaïsme, le triangle et la pyramide sont des symboles maçonniques, etc.

Même les solides de Platon ont été revêtus, par des auteurs ésotériques, de pouvoirs et de vertus magiques, et bien des auteurs ont recherché des applications du nombre d’or un peu partout, sur les monuments, les sculptures et les dessins.

Aujourd’hui, leur sens est aussi devenu politique. Si seulement leur magie pouvait suffire à réunir les humains – ne serait-ce que pour la gloire de la géométrie…

Maroc, Israël, Danemark… si proches!

La Spirale universelle

Nous avons mentionné ci-dessus l’universalité de la spirale, simple, double ou triple. En voici quelques exemples.

Quand l’oeil de la Providence louche vers la banque américaine…

Puissant symbole dans bien des cultures (en commençant par l’Egypte, avec l’oeil Oudjat ou « oeil d’Horus »), oeil porte-bonheur sur les amulettes et à l’avant des navires, religieux quand il se voile dans les nuées ou les rayons du soleil, humaniste et maçonnique quand il s’inscrit dans un triangle, 

l’endroit le plus inattendu où l’on peut le trouver est bien… dans cet autre symbole d’un monde infiniment matérialiste : le billet de 1 dollar américain. Et perché sur une pyramide, qui plus est !

Quant au Triskell celtique…